The figure below gives the behavior of the derivative of on
.
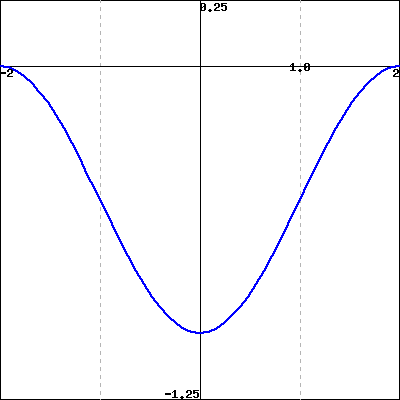 Graph of (not )
(Click on the graph to get a larger version.)
Graph of (not )
(Click on the graph to get a larger version.)
Sketch a graph of and use your sketch to answer the following
questions.
A.
Where does the graph of have inflection points?
Enter your answer as a comma-separated list of values, or enter
none if there are none.
B.
Where are the global maxima and minima of on ?
minimum at
maximum at
C.
If , what are possible values for ?
is in
(Enter your answer as an interval, or union of intervals, giving
the possible values. Thus if you know , enter
(-5,-2]. Enter infinity for
, the interval [1,1] to indicate a single
point).
How is the value of related to the value of ?
(Enter the appropriate mathematical equality or inequality,
, , , etc.)